[수학] 사이클로이드 곡선의 성질 정리 (넓이, 길이, 회전체, 접선 등등)
[수학] 사이클로이드 곡선의 성질 정리 (넓이, 길이, 회전체, 접선 등등)
안녕하세요 수학올인입니다.
이번 포스팅에서는 사이클로이드 곡선에 대해서 다뤄보겠습니다.
우리가 고등학교를 다닐 때 다항함수들의 넓이나 접선같은 성질에 대해 탐구했던 것처럼,
사이클로이드 곡선에 대해서도 많은 성질들이 있는데요.
제목과 같이 사이클로이드 곡선의 넓이나 길이, 회전체의 부피나 겉넓이, 마지막으로 기하학적 성질들을
전부 정리해서 이번 포스팅에서 다뤄보겠습니다.
사이클로이드 곡선의 정의?
사이클로이드 곡선 (파선)은 반지름의 길이가 $a$인 원을 직선 위에서 굴렸을 때,
원 위의 한 점이 그리는 자취가 나타내는 곡선을 말합니다.
그런데 아마 이 글을 읽으시는 독자분들은 위와 같은 정의에는 별로 관심이 없을 것이라 예상합니다.
따라서 바로 식으로 들어가보면, 사이클로이드 곡선이란 양수 $a$에 대하여 다음과 같은 매개변수로 정의된 곡선을 말합니다.
$$r(t)=(a(t-\sin t), a(1- \cos t))$$
그리고 그래프를 그려보면 아래 사진과 같습니다.

위 그래프는 $0\leq t\leq 2\pi$에서 그린 매개곡선 $r(t)$의 그래프입니다.
물론 $t$의 값이 이보다 더 크다면 오른쪽으로도 쭉쭉 그림이 그려질텐데요.
주로 $t$의 범위를 막 키워서 생각하는 경우는 많지는 않고
이 그림처럼 $0\leq t\leq 2\pi$에서만 다루는 경우가 많습니다. (이를 사이클로이드 곡선의 한 아치라고 합니다.)
그럼 이 그림을 바탕으로 사이클로이드 곡선의 기하학적 성질부터 알아볼게요.
사이클로이드 곡선의 기하학적 성질
다양한 성질이 있겠지만, 제가 주목하는 것은 사이클로이드 곡선의 접선입니다.
먼저 아래 사진을 보겠습니다.
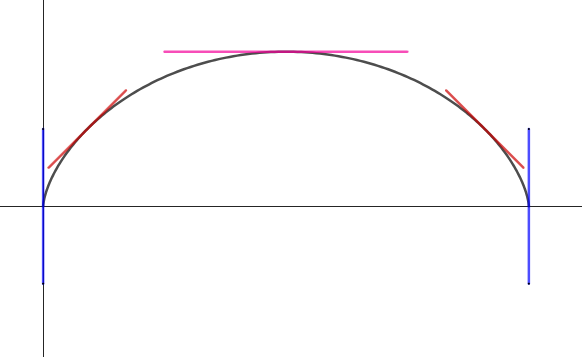
다음이 성립합니다.
1. 사이클로이드 곡선의 한 아치 ($0\leq t\leq 2\pi$)는 $x=\pi$에 대하여 선대칭입니다.
2. $t=0, t=2\pi$에서의 접선은 수직접선입니다. (파란색)
3. $t=\frac{\pi}{2}, t=\frac{\pi}{3}$에서의 접선의 기울기는 각각 $1, -1$입니다. (빨간색)
($x$가 아닌 $t$임에 주의!)
4. $t=\pi$에서의 접선의 기울기는 $0$입니다. (분홍색)
증명은 매개변수로 정의된 함수의 미분을 통해 어렵지 않게 할 수 있습니다.
3번의 경우 편입시험과 같은 시험에서 은근히 물어보는 경우가 있습니다.
또, 위의 성질들은 앞에 곱해진 $a$의 값에 관계없이 성립하는 성질입니다.
사이클로이드 곡선의 넓이
위에서 사이클로이드 곡선의 한 아치가
$$r(t) = (a(t-\sin t), a(1-\cos t))\quad (0\leq t\leq 2\pi)$$
라고 하였는데, 이 곡선과 $x$축이 이루는 넓이는 얼마일까요?
그 값은 $3a^2 \pi$입니다. 증명은 아래와 같습니다.
$$\begin{align} S &= \int_0^{2\pi} y dx \\ &= \int_0^{2\pi} y \frac{dx}{dt} dt \\ &= \int_0^{2\pi} a(1-\cos t) \times a(1-\cos t)dt \\ &= 3a^2 \pi \end{align}$$
만약 한 아치가 아닌 여러 아치의 값을 물어본다면 적당히 여러번 세주면 되겠습니다.
또, 만약 한 아치의 절반의 넓이를 물어본다면 대칭성을 이용하면 되겠습니다.
사이클로이드 곡선의 길이
이번에는 단도직입적으로 말하면 사이클로이드 곡선의 한 아치의 길이는 $8a$입니다.
증명은 아래와 같습니다.
$$\begin{align} L &= \int_0^{2\pi} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} dt \\ &= \int_0^{2\pi} a\sqrt{2 - 2\cos x}dx \\ &= 8a\end{align}$$
마찬가지로 여러 아치의 길이를 물어본다면 대칭성을 이용하고, 절반의 경우 대칭성을 이용합니다.