[수학] 반원과 사분원의 내부 및 그 호의 질량중심
[수학] 반원과 사분원의 내부 및 그 호의 질량중심
안녕하세요 수학올인입니다.
이번 포스팅에서는 원 및 원 호의 질량중심에 대해 다뤄보겠습니다.
별도의 밀도함수가 없다고 가정하고, 원의 질량중심과 원 호의 질량중심은 주로 회전체의 부피나
회전체의 겉넓이를 구할 때 파푸스의 정리와 함께 이용됩니다.
일반적인 시험에서는 잘 이용되지 않고, 편입 수학과 같이 시간 제한이 타이트한 경우 주로 이용하구요.
결론적으로 반구의 부피 및 반구면의 겉넓이를 구할 때 이용될 수 있습니다.
이번 포스팅에서는 반원 및 사분원인 경우만 다루며, 그 일부분이 정확히 제 1, 2, 3, 4사분면의
한 영역 또는 두 영역에만 포함된다고 가정하겠습니다.
반원과 사분원 내부의 질량중심
우선 완벽한 원의 질량중심은 당연하게도 원의 중심과 같습니다.
그렇다면 반원의 질량중심은 어떻게 구할 수 있을까요?
보통 질량중심을 구할 때 이중적분을 이용하여 질량중심 공식을 이용하지만,
이번 포스팅에서 구할 모든 질량중심은 이중적분을 이용하지 않을 것입니다.
그 이유는, 앞서 말 한 것처럼 질량중심을 구한 뒤 파푸스의 정리를 통해 회전체의 부피 및 겉넓이를 구한다고 했는데
원의 일부분을 회전시키면 구가 되고, 우리는 구의 부피 및 겉넓이를 이미 알고 있기 때문에
파푸스의 정리를 역으로 적용하여 질량중심을 뽑아낼 수 있는 것이죠.
그럼 가장 간단한 경우인 중심이 원점이고 반지름이 $r$인 원
$$x^2 + y^2 \leq r^2$$
의 상반원인
$$y\geq 0, x^2 + y^2 \leq r^2$$
의 질량중심을 구해보겠습니다. 우선 이 도형은 $y$축에 대칭이므로, 질량중심의 $x$좌표는 당연히 $0$일 것입니다.
그러면 $y$좌표를 구해주면 되는데, 우선 아직 모르는 상태이니 $a$라고 둬보겠습니다.
이때 이 상반원을 $x$축을 중심으로 회전시키면 반지름이 $r$인 구가 되고, 이 구의 부피 $V$는
$$V = \frac{4}{3}\pi r^3$$
이 됨을 이미 알고 있습니다.
따라서 이 부피 $V$를 파푸스의 정리를 이용하여 구했다고 생각하면
$$V = 2\pi \times \frac{\pi}{2}r^2 \times a$$
라고 쓸 수 있고, 식을 정리하면
$$a = \frac{4r}{3\pi}$$
임을 바로 얻을 수 있습니다.
이제 대칭성을 이용하면 상반원이 아닌 하반원의 경우 부호만 바꿔주면 되고
원을 위 아래가 아닌 좌 우를 기준으로 절반을 나눈 경우 질량중심의 $y$좌표는 $0$이고 $x$좌표가
오른쪽의 경우 부호가 +, 왼쪽의 경우 부호가 -가 될 것이구요.
만약 중심이 원점이 아니라면? 그만큼 평행이동을 해줬다고 생각하면 됩니다.
그렇다면 반원이 아닌 사분원의 경우는 어떻게 될까요?
중심이 원점, 반지름이 $r$이고 제 1, 2, 3, 4사분면 중 정확히 한 곳에만 딱 포함되는 사분원이 있다고 해봅시다.
예시로
$$x\geq 0, y\geq 0, x^2 + y^2 \leq r^2$$
을 들어볼게요.
이 경우는 별도의 대칭성이 없으므로 질량중심의 좌표를 $(a, b)$로 두겠습니다.
위와 비슷한 과정을 이용할 것인데, 이 영역을 $x$축 또는 $y$축으로 회전시키면 반지름이 $r$인 반구가 되고
이 구의 부피 $V$는
$$V = \frac{2}{3}\pi r^3$$
임을 알고 있습니다.
이제 이를 파푸스의 정리를 통해 구했다고 생각하면
$$\begin{align} V &= 2\pi \times a \times \frac{\pi}{4}r^2 \\ &= 2\pi \times b \times \frac{\pi}{4}r^2 \end{align}$$
라고 쓸 수 있습니다. 뒤의 등식이 성립하는 이유는 $x$축을 중심으로 회전시키든 $y$축을 중심으로 회전시키든
부피가 같은 반구가 나오기 때문입니다. 이를 풀어서 쓰면
$$a=b=\frac{4r}{3\pi}$$
가 됩니다.
마찬가지로 사분원의 경우도 해당 사분원이 어떤 사분면에 위치하는지에 따라 부호만 적절히 결정해주면 됩니다.
따라서 위에서 얻은 반원 및 사분원 내부의 질량중심을 정리하면 다음과 같습니다.

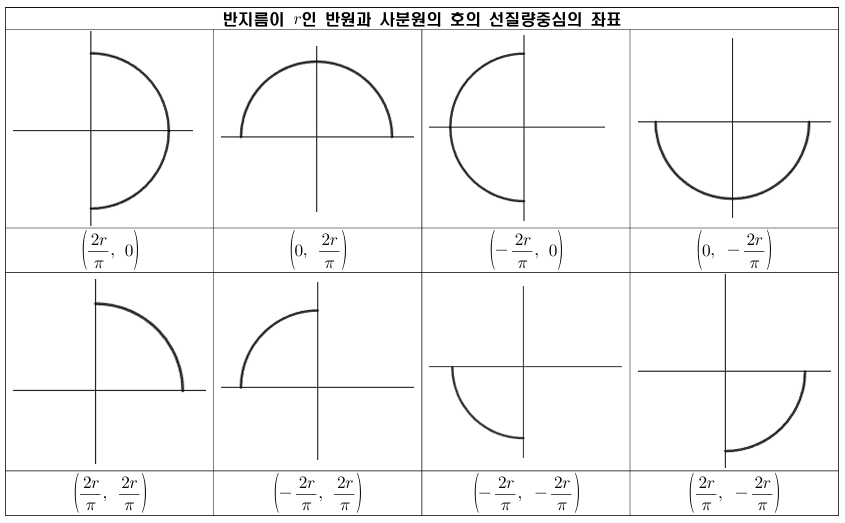
반원과 사분원의 호의 선질량중심
그렇다면 이번에는 반원 또는 사분원의 내부가 아닌 그 원 호의 질량중심은 어떻게 구할 수 있을까요?
그 방식은 아주 비슷한데 단순히 구의 부피가 아닌 구의 회전체의 겉넓이에 대해 완전히 같은 논리를 적용합니다.
마찬가지로 중심이 원점이고, 반지름이 $r$인 원
$$x^2 + y^2 = r^2$$
의 상반원의 원 호인
$$x^2 + y^2 = r^2, y\geq 0$$
을 생각해보겠습니다.
이전과 동일하게 $y$축에 대칭임을 이용하면 선질량중심의 $x$좌표는 $0$일 것이고
$y$좌표를 $a$라 하겠습니다.
이 도형을 $x$축을 중심으로 회전시킨 도형은 반지름이 $r$인 구가 되고, 이 구의 겉넓이 $S$는
$$S = 4\pi r^2$$
임을 이미 알고 있습니다.
이를 파푸스의 정리를 통해 구했다고 생각해보면
$$S = 2\pi \times a \times \pi r$$
에서 식을 정리하면
$$a = \frac{2r}{\pi}$$
임을 얻습니다.
위와 마찬가지로 위가 아닌 아래라면 부호가 -, 상 하가 아닌 좌 우로 나뉜 경우 $y$좌표가 $0$이고 $x$좌표를
구한 $a$값과 동일하게 주되, 오른쪽 부분의 경우 부호를 +, 왼쪽 부분의 경우 부호를 -로 주면 됩니다.
그럼 사분원의 호는 어떻게 될까요? 사분원의 내부를 구할 때 처럼 선질량중심의 좌표를 $(a, b)$라 써보겠습니다.
이제 반원의 호의 질량중심을 구한 과정을 동일하게 적용한 뒤 반구의 겉넓이를 이용하면 되고,
이미 동일한 논리를 이용하는 과정을 여러번 반복했으니 과정을 생각하고 결론만 적으면
$$a=b=\frac{2r}{\pi}$$
임을 얻습니다.
사분원의 내부의 질량중심의 경우와 마찬가지로 사분면의 위치에 따라 부호만 적당히 조절해주면 되고요.
이를 정리하면 다음과 같습니다.
그럼 이상으로 포스팅을 마치겠습니다.
오류, 오타 또는 궁금하신 점이 있으시면 댓글로 남겨주세요~