2025학년도 6월 모의고사 수학(미적분) 29번 풀이 (250629 풀이)

안녕하세요 수학올인입니다.

이번 포스팅에서는 2025학년도 6월 모의고사 수학(미적분) 29번 문제를 다뤄보겠습니다.

먼저 미분해보면

$$\begin{align} f'(x) &= x^2 - 2x + \frac{2x}{x^2 + 1} \\ &= \frac{x^4 - 2x^3 + x^2}{x^2 + 1} \\ &= \frac{x^2 (x-1)^2}{x^2 + 1} = 0\end{align}$$

에서 $f'(0)=f'(1)=0$이고, $f'(x) \geq 0$이므로 함수 $f$는 증가한다.

이를 바탕으로 $y=f(x)$의 개형을 대략적으로 그리면 다음과 같다.

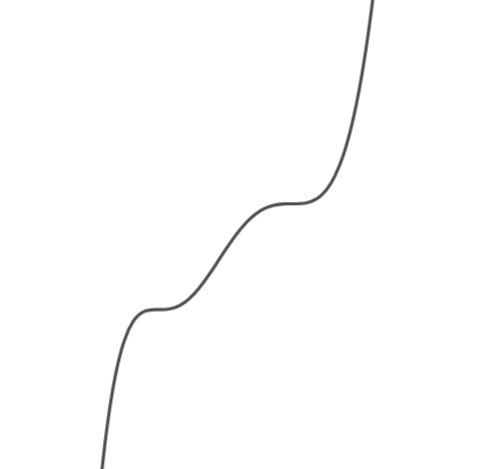
이제, $y$의 값은 고려하지 않고 (어차피 $y$값은 $a$를 조절해서 맞춰주면 되니까)

어떤 상황에서 미분가능하게 할 수 있는지를 먼저 확인해보자.

함수 $g$는 함수 $f$를 평행이동 시킨 뒤 $x$축에 대칭이동을 시킨 것을 원래의 $f$와 합쳐놓은 그래프인데

$x$축에 대칭이동 시킨것이 원래의 함수와 겹쳣을 때 미분가능해야하므로 $b=1$이다.

($b$가 양수이므로 $0$은 될 수 없다.)

그럼 자연스럽게 기울기가 $0$인 지점인 $x=0$를 평행이동시켜 $x=1$에 위치시켜야 하므로 $c=1$이다.

기울기에 대해서는 전부 따졌으므로, 함숫값에 대해 따져보면 $x$축에 대칭시키기 전과 그 후가 일치하려면

대칭시키기 전과 후는 절댓값이 같고 부호만 다른 상황이다. 즉 $f(0) = -f(1)$이라는 뜻이다.

따라서 $f(0) + f(1) = 0$이어야 하므로

$$f(0)+f(1) = 0 \quad \Longrightarrow\quad a=\frac{1}{3} - \frac{1}{2}\ln 2$$

이다.

위에서 얻은 정보를 종합하면

$$a+b+c=\frac{7}{3} - \frac{1}{2}\ln 2$$

이므로

$$30(p+q) = 55$$

이다.

무난한 미분가능성 문항인데요, 절댓값도 없고 적당한 수준의 평행이동 및 대칭이동만을 물어봐서

특수한 상황을 기준으로 나누면 바로 해결됩니다.