[편입] 2024 가천대학교 편입수학 기출문제 정답 및 해설 (풀이)
안녕하세요 수학올인입니다.
이번 포스팅에선 2024년 가천대학교 편입수학 기출문제의 정답과 풀이를 다뤄보겠습니다.
풀이는 전부 제 풀이이며, 따라서 오타나 오류가 있을 수 있습니다.
원본 시험지는 제가 공유하지 않으며, 세종대학교 입학처에서 확인하실 수 있습니다.
(가천대학교 입학처 - 편입학 - 공지사항)
2024년도가 아닌 다른 년도의 정답 및 해설은 글 가장 아래에 정리되어 있습니다.
2024 가천대학교 편입수학 기출문제 빠른 정답
빠른 정답은 위 사진을 참고해 주시고, 아래는 문항별 풀이입니다.
2024 가천대학교 편입수학 기출문제 1번 풀이
$x=0$근방에서 $\tan x\approx x$이므로 구하는 극한값은
$$\lim_{x\to 0+}x^x = 1$$
로 근사시켜 계산할 수 있다.
2024 가천대학교 편입수학 기출문제 2번 풀이
구하는 길이 $L$은
$$\begin{align}
L &= \int_2^4 \sqrt{1+(f'(x))^2}dx \\
&= \int_2^4 xdx \\
&= 6
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 3번 풀이
복잡하게 함수들이 곱해진 경우 로그미분법을 이용한다. $f(0)=4$이고, 양변에 자연로그를 취하면
$$\ln f(x) = 2\ln(x^3 + 2) + 4x + \ln \cos(5\tan x) - \frac{1}{2}\ln(x^3 + 1)$$
이다.
이제 미분하기 전에 잘 살펴보면 $4x$를 제외한 모든 항은 미분했을 때 기울기가 $0$이다.
따라서 우리는 양변을 미분한 뒤 $x=0$을 넣을 것이므로, 나머지 항은 전부 무시하고 우변에 $4x$만 남긴채 계산한다.
양변을 미분하면
$$\frac{f'(x)}{f(x)} = 4$$
에서
$$f'(0)=4f(0)=16$$
이다.
2024 가천대학교 편입수학 기출문제 4번 풀이
$x=\sin t$로 치환하면 주어진 적분은
$$\begin{align}
\text{(Integral)} &= \int_0^{\frac{\pi}{2}}\sin^2 t\cos^2 t dt \\
&= \int_0^{\frac{\pi}{2}}(\sin^2 t - \sin^4 t)dt \\
&= \frac{\pi}{4} - \frac{3}{16}\pi \\
&= \frac{\pi}{16}
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 5번 풀이
구하는 식과 선택지를 잘 살펴보면, 선택지의 $4e^{\frac{8}{3}\pi}$는 전부 공통으로 들어가있다.
한편 이 $4e^{\frac{8}{3}\pi}$라는 항은 $x=e^{2t}$를 대입했을 때 생긴다.
근데 어차피 모든 선택지에 저게 포함되어 있으므로 저 항은 무시하고 나머지만 계산해도 된다.
즉,
$$w = y^2 + 2z^2 = 1+\sin^2 t$$
이므로
$$\frac{dw}{dt} = 2\sin t\cos t$$
이다. 따라서 이 상태에서 $t=\frac{2}{3}\pi$를 대입하면 $-\frac{\sqrt{3}}{2}$이고, 이를 포함하는 선택지는 2번이다.
2024 가천대학교 편입수학 기출문제 6번 풀이
함수 $p(x)$를
$$p(x) = x^3 - 3x$$
라 하면, $x=-1$에서 극댓값 $2$, $x=1$에서 극솟값 $-2$를 가지고 $f(-2)=-2, f(2)=2$를 만족시킨다.
이제 곡선 $y=p(x)$와 정수 $n$에 대하여 $y=n$을 그어놓고
i) $y=p(x)$가 $y=n$을 뚫고 가는 지점
ii) $y=p(x)$가 위로 볼록한 형태로 $y=n$과 접하는 지점
의 개수를 구하면 함수 $f(x)$가 불연속인 지점의 개수와 일치한다.
위와 같이 그림을 그릴 수 있고, 불연속점의 개수는 10이다.
2024 가천대학교 편입수학 기출문제 7번 풀이
양변을 $y^2$으로 나누면 주어진 미분방정식은
$$y'+\frac{y}{x}=\frac{2}{x^2}y^{-2}$$
이고 이는 베르누이 미분방정식이다. $y=u^3$으로 치환하면 주어진 미분방정식은
$$u' + \frac{3}{x}u = \frac{6}{x^2}$$
이고 이는 일계 선형 미분방정식이므로 공식을 이용하면
$$\begin{align}
u &= \frac{1}{x^3}\left(\int 6xdx + C\right) \\
&= \frac{3x^2 + C}{x^3} \\
&= y^3
\end{align}$$
에서
$$y=\frac{\sqrt[3]{3x^2 + C}}{x}$$
이고, $y(1)=2$이므로 $C=5$이다. 따라서
$$\begin{align}
y\left(\frac{1}{2}\right) &= 2\times \left(\frac{23}{4}\right)^{\frac{1}{3}} \\
&= 2^{1-\frac{2}{3}} \times 23^{\frac{1}{3}} \\
&= 46^{\frac{1}{3}}
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 8번 풀이
주어진 식의 양변을 $\theta$로 미분해보면
$$r'(\theta) = 8\sin^2\left(\frac{\theta}{3}\right)\cos\left(\frac{\theta}{3}\right)$$
이다. 따라서 구하는 길이 $L$은
$$\begin{align}
L &= \int_0^{\frac{\pi}{4}} \sqrt{r^2 + (r')^2}d\theta \\
&= \int_0^{\frac{\pi}{4}} \sqrt{64\sin^4 \left(\frac{\theta}{3}\right)}d\theta \\
&= 8\int_0^{\frac{\pi}{4}} \sin^2\left(\frac{\theta}{3}\right)d\theta \\
&= 4\int_0^{\frac{\pi}{4}} \left(1-\cos\left(\frac{2\theta}{3}\right)\right)d\theta \\
&= \pi+3
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 9번 풀이
벡터 $b$는 행렬 $A$의 1열이다. 따라서
$$\hat{x} = \begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}$$
이므로, 모든 성분의 합은 1이다.
2024 가천대학교 편입수학 기출문제 10번 풀이
문제의 조건으로부터 주어진 멱급수는
i) $-3<x\leq 3$에서 수렴
ii) $x\leq -5$, $x>5$에서 발산
임을 알 수 있다. 이제 보기를 보면
ㄱ. $x=1$인 경우이므로 수렴한다.
ㄴ. $x=6$인 경우이므로 발산한다.
ㄷ. $x=-2$인 경우이므로 수렴한다.
ㄹ. $x=-8$인 경우이므로 발산한다.
이상에서 수렴하는 급수의 개수는 2이다.
2024 가천대학교 편입수학 기출문제 11번 풀이
주어진 행렬 $A$의 고유치는
$$\lambda = 7, 7, 2$$
이고, 각각에 대응되는 고유벡터는
$$\begin{pmatrix}
1 \\
-2 \\
0
\end{pmatrix}, \begin{pmatrix}
1 \\
0 \\
1
\end{pmatrix}, \begin{pmatrix}
2 \\
-1 \\
2
\end{pmatrix}$$
이다.
이제 행렬 $P$는 행렬 $A$의 고유벡터를 열로 가져야 하는데, 모든 정보가 있는 2열을 보면
우리가 구한 고유벡터와 일치하는 것이 없다.
이때 고유치 $\lambda = 7$의 고유공간의 차원이 2라는 것에 주목해야 하는데, $\lambda=7$에 대응되는
두 개의 고유벡터의 일차결합을 통해 $P$의 2열과 평행한 벡터를 만들 수 있기 때문이다.
구체적으로는
$$\begin{pmatrix}
4 \\
2 \\
5
\end{pmatrix} = 5\begin{pmatrix}
1 \\
0 \\
1
\end{pmatrix} - \begin{pmatrix}
1 \\
-2 \\
0
\end{pmatrix}$$
로 표현할 수 있다. (이 문제에서는 표현까지 할 필요는 없다. 고유치 7에 대응되는 벡터라는거만 알면 된다.)
그럼 나머지 1열과 3열을 채우자. $\lambda = 2$에 대응되는 벡터는 세 번째 성분이 $0$이 아니므로
1열에는 들어갈 수 없다. 따라서 3열에 들어가야 하고, 크기를 $1$로 만들어주면
$$\begin{pmatrix}
c \\
d \\
e
\end{pmatrix} = \frac{1}{3}\begin{pmatrix}
2 \\
-1 \\
2
\end{pmatrix}$$
이다.
이제 1열에는 $\lambda=7$에 대응되는 고유벡터가 들어가야 하는데, 세 번째 성분이 $0$이므로, 크기를 1으로 만들어주면
$$\begin{pmatrix}
a \\
b \\
0
\end{pmatrix}= \frac{1}{\sqrt{5}}\begin{pmatrix}
1 \\
-2 \\
0
\end{pmatrix}$$
이다. 이상에서
$$\begin{cases}
a +b &= -\frac{1}{\sqrt{5}} \\
c+d+e &= \frac{1}{3}
\end{cases}$$
이므로, 구하는 값은
$$a+b+c+d+e=\frac{1}{3}-\frac{1}{\sqrt{5}}$$
이다.
2024 가천대학교 편입수학 기출문제 12번 풀이
곡면 $S$는 폐곡면이다. 곡면 $S$의 내부를 $E$라 하고 발산정리를 이용하면 주어진 면적분은
$$\begin{align}
\text{(Integral)} &= \iiint_E 2z dV \\
&= \iint_{x^2 + y^2 \leq 4} (4-x^2-y^2)dA \\
&= \int_0^{2\pi}\int_0^2 r(4-r^2)drd\theta \\
&= 8\pi
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 13번 풀이
미분한 순서대로 적분하면 주어진 이중적분은
$$\begin{align}
\text{(Integral)} &= \int_0^1 (f_y(1,y)-f_y(0,y))dy \\
&= f(1,1)-f(1,0)-f(0,1)+f(0,0) \\
&= \frac{\pi}{4}+2024-\frac{2024}{e}
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 14번 풀이
일단 $v_1=w_1$로 골랐음은 바로 알 수 있다. 이제
$$v_2 = u_2 - \text{proj}_{v_1}u_2 = \begin{pmatrix}
-\frac{1}{3} \\
\frac{1}{6} \\
\frac{1}{6}
\end{pmatrix}$$
임을 얻고, $v_3$는 $v_1$와 $v_2$를 외적하여 구하자.
어차피 크기를 따로 맞춰주어야 하므로 $v_1$와 $6v_2$를 외적하면
$$v_3 = \begin{pmatrix}
0 \\
-3 \\
3
\end{pmatrix}$$
이 나오는데, 문제에서 주어진 $v_3$은 첫번째 성분이 $0$이 아니다.
따라서 구하는 순서를 바꿔야 한다. 위에서 $v_2$를 구할 때 $w_2$를 이용했는데, 그게 아니라 $w_3$을 이용하면
$$v_2 = u_3 - \text{proj}_{v_1}u_3 = \begin{pmatrix}
-\frac{1}{3} \\
-\frac{1}{3} \\
\frac{2}{3}
\end{pmatrix}$$
임을 얻고, 마찬가지로 $v_3$는 외적을 이용하여 $v_1$와 $-3v_2$를 외적한 뒤 크기를 맞춰주면
$$v_3 = \begin{pmatrix}
-\frac{1}{2} \\
\frac{1}{2} \\
0
\end{pmatrix}$$
으로 문제의 조건에 전부 부합한다.
따라서
$$a=-\frac{1}{3}, b=\frac{2}{3}, c=\frac{1}{2}, d=0$$
이므로
$$3a+2b+2c+d=\frac{4}{3}$$
이다.
2024 가천대학교 편입수학 기출문제 15번 풀이
역연산자와 소멸연산자를 통해 특수해를 먼저 구해보면
$$\begin{align}
y_p &= \frac{1}{D^2 +9 }\left\{2\sin 3x\right\} \\
&= -\frac{1}{3}x\cos 3x
\end{align}$$
이다.
따라서 제차해 $y_c$는 미분방정식
$$y''+9y=0, \quad y_c(0)=1, y_c'(0)=2$$
를 만족시키고, 이는 라플라스 변환을 통해 해결할 수 있다.
$y_c$의 라플라스 변환을 $Y$라 하고 양변을 라플라스 변환하면
$$Y = \frac{s+2}{s^2 + 9}$$
에서 역변환하면
$$y_c = \frac{2}{3}\sin 3x + \cos 3x$$
이다. 따라서 주어진 미분방정식의 해는
$$\begin{align}
y &= y_c + y_p \\
&= \frac{2}{3}\sin 3x + \cos 3x -\frac{1}{3}x\cos 3x
\end{align}$$
이므로
$$y\left(\frac{\pi}{2}\right) = -\frac{2}{3}$$
이다.
2024 가천대학교 편입수학 기출문제 16번 풀이
주어진 영역의 내부와 경계로 나누어 구하자.
i) 영역 내부
임계점을 구하면
$$\begin{cases}
f_x &= 2x-2y-4 = 0 \\
f_y &= 8y-2x-2=0
\end{cases}$$
에서 $(x,y)=(3,1)$이고, $f(3,1)=17$이다.
ii) 경계 : $y=-2, 0\leq x\leq 4$
$$f(x,-2)=x^2 + 44$$
이므로 최소는 44, 최대는 60이다.
iii) 경계 : $x=4, -2\leq y\leq 2$
$$f(4, y)=4y^2 - 10y + 24$$
이므로 최소는 $\frac{71}{4}$, 최대는 60이다.
iv) 경계 : $y=2, 0\leq x\leq 4$
$$f(x, 2)=x^2 - 8x + 36$$
이므로 최소는 20, 최대는 36이다.
v) 경계 : $x=0, -2\leq y\leq 2$
$$f(0, y) = 4y^2 - 2y + 24$$
이므로 최소는 $\frac{95}{4}$, 최대는 44이다.
위를 전부 종합하면 $M=60, m=17$이므로 $M+m=77$이다.
2024 가천대학교 편입수학 기출문제 17번 풀이
ㄱ. 비율판정법으로부터 수렴한다.
ㄴ. 지수 로그의 성질을 이용하면
$$\begin{align}
(\ln n)^{\ln n} &= e^{\ln n \ln \ln n} \\
&=n^{\ln \ln n}
\end{align}$$
이다. 이제 어떤 $n$부터는 항상 $\ln \ln n > 2$이도록 할 수 있으므로, 어떤 $n$부터는 항상
$$n^{\ln \ln n} > n^2$$
이도록 할 수 있다. 이제 양변을 역수취하면
$$0<\frac{1}{n^{\ln \ln n}} < \frac{1}{n^2}$$
이므로, 비교판정법으로부터 수렴한다.
ㄷ. 마찬가지로 지수 로그의 성질을 이용하면
$$(\ln n)^{\ln \ln n} = e^{(\ln \ln n)^2}$$
이다. 이제 부등식
$$\ln x< \sqrt{x}$$
가 성립함을 이용할 것인데, $x$대신 $\ln n$을 대입한 뒤 양변을 제곱하면
$$(\ln \ln n)^2 < \ln n$$
임을 얻는다. 이 부등식을 위의 식에 적용하면
$$\begin{align}
(\ln n)^{\ln \ln n} &= e^{(\ln \ln n)^2} \\
&< e^{\ln n} \\
&= n
\end{align}$$
이다. 즉,
$$(\ln n)^{\ln \ln n} < n$$
이므로, 양변을 역수취하면
$$\frac{1}{(\ln n)^{\ln \ln n}} > \frac{1}{n}$$
이다. 따라서 비교판정법으로부터 발산한다.
ㄹ. $\ln n < \sqrt{n}$이므로 비교판정법과 $p$급수 판정법으로부터 수렴한다.
이상에서 수렴하는 급수의 개수는 3이다.
2024 가천대학교 편입수학 기출문제 18번 풀이
극좌표계를 이용하면 주어진 이중적분은
$$\begin{align}
\text{(Integral)} &= \int_0^{\frac{\pi}{4}}\int_0^2 \frac{r}{1+r^2}drd\theta \\
&= \frac{\pi}{8}\ln 5
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 19번 풀이
각각의 행벡터를 행으로 하는 $4\times 4$크기의 행렬식 또는 $\text{rank}$를 조사하면 된다.
이 포스팅에서는 $\text{rank}$를 조사할 것이고, 각각 구해보면
ㄱ. $\text{rank} = 4$
ㄴ. $\text{rank} = 4$
ㄷ. $\text{rank} = 3$
이다. 이상에서 일차독립인 집합의 개수는 ㄱ, ㄴ으로 2이다.
2024 가천대학교 편입수학 기출문제 20번 풀이
모든 양수 $x$에 대하여
$$\cot^{-1}x = \frac{\pi}{2}-\tan^{-1}x$$
가 성립함을 이용하자. 양변을 제곱하면
$$(\cot^{-1}x)^2 = \frac{\pi^2}{4} - \pi\tan^{-1}x + (\tan^{-1}x)^2$$
이므로, 이를 대입한 뒤 부분적분을 이용하면 주어진 적분은
$$\begin{align}
\text{(Integral)} &= -\int_0^1 \left(\frac{\pi^2}{4}- \pi\tan^{-1}x\right)dx \\
&= -\frac{\pi}{2}\ln 2
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 21번 풀이
행렬 $A$의 고유치를 $a, b, c$라 하면, 행렬 $A^{-1}$의 고유치는 행렬 $A$의 고유치의 역수이므로
$$\begin{align}
\text{tr}(A^{-1}) &= \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \\
&= \frac{ab+bc+ca}{abc} \\
&= \frac{C_{11} + C_{22} + C_{33}}{\det A } \\
&= \frac{1 - 15 - 24}{1} \\
&= -38
\end{align}$$
이다. 이때 $C_{ij}$는 행렬 $A$의 $i$행 $j$열 성분에 대한 여인수이다.
2024 가천대학교 편입수학 기출문제 22번 풀이
구하는 직선의 방향벡터는 주어진 점에서 두 곡면 및 평면의 경도벡터의 외적이다.
계산해보면 $a=3, b=-4$이므로 구하는 값은 $|a+b|=1$이다.
2024 가천대학교 편입수학 기출문제 23번 풀이
이 포스팅에서는
i) 일반적인 직선인 $y=mx+n$에 대한 회전체의 부피를 구하는 공식을 이용한 풀이
ii) 무게중심의 좌표를 구한 뒤 파푸스의 정리를 이용한 풀이
를 모두 소개한다.
[풀이 1]
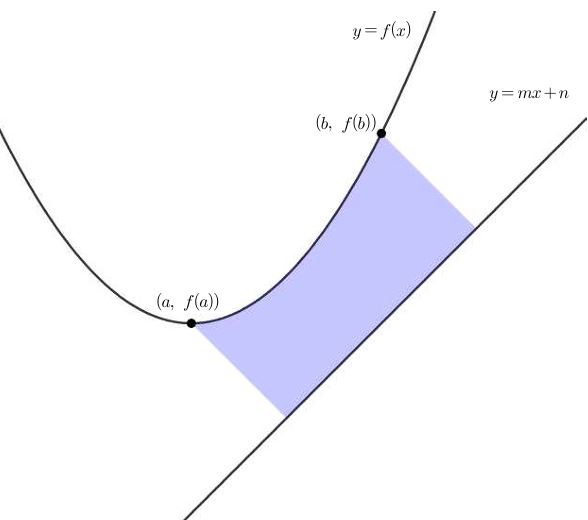
위의 그림과 같은 상황을 생각하자.
이때 그림의 파란색 영역을 직선 $y=mx+n$을 중심으로 회전시켜 얻은 회전체의 부피 $V$는
$$V=\frac{\pi}{(1+m^2)^{\frac{3}{2}}}\int_a^b (f(x)-mx-n)^2(1+mf'(x))dx$$
이다.
이를 이용하면, $a=0, b=2$이고, 회전의 중심이 되는 직선은 $y=4x$이므로 구하는 부피 $V$는
$$\begin{align}
V &= \frac{\pi}{17\sqrt{17}}\int_0^2 (x^3 - 4x)^2(1+12x^2)dx \\
&= \frac{1024\pi}{17\sqrt{17}}
\end{align}$$
이므로 정답은 3번이다.
[풀이 2]
파푸스의 정리를 이용하기 위해 $y=4x$와 $y=x^3$으로 둘러싸인 영역의 무게중심을 구하자.
이 영역의 넓이가 $4$이므로, 무게중심 공식을 이용하면
$$\begin{align}
\bar{x} &= \frac{1}{4}\int_0^2\int_{x^3}^{4x} xdydx = \frac{16}{15} \\
\bar{y} &= \frac{1}{4}\int_0^2\int_{x^3}^{4x} ydydx = \frac{64}{21}
\end{align}$$
이다. 이제 무게중심과 직선 $y=4x$사이의 거리 $d$는
$$d= \frac{128}{105\sqrt{17}}$$
이므로 파푸스의 정리를 이용하면 구하는 부피 $V$는
$$V = 2\pi \times d\times 4 = \frac{1024\pi}{17\sqrt{17}}$$
이다.
2024 가천대학교 편입수학 기출문제 24번 풀이
문제에서 주어진 영역이 대칭성을 띄므로, 구하는 이중적분의 값은 제 1사분면에서의 이중적분값의 4배이다.
또, 제 1사분면 내부에서도 $y=x$를 기준으로 대칭성을 띄므로 구하는 이중적분의 값은 제 1사분면 중 $y=x$보다
아래에 있는 영역에서의 이중적분값의 8배이다.
이제 사진과 같이 영역을 나눌 수 있다.
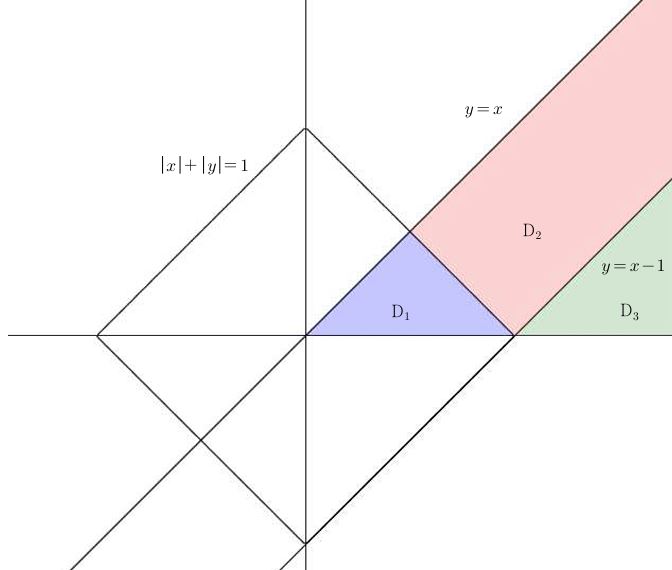
i) 파란색 영역 $D_1$의 경우, 이미 영역 내부에 있으므로
$$f(x,y)=0$$
이다. 따라서
$$\iint_{D_1} e^{-f(x,y)}dA = \frac{1}{4}$$
이다.
ii) 빨간색 영역 $D_2$의 경우, 빨간색 영역 내부에 아무런 점이나 고른 뒤, 고른 점을 중심으로하는 원을 그려서
반지름을 조금씩 키워가다보면 $y=1-x$에 가장 먼저 닿게됨을 알 수 있다. 따라서 영역 $D_2$에서 함수 $f(x,y)$는
점 $(x, y)$와 직선 $y=1-x$사이의 거리와 같으므로
$$f(x,y)=\frac{x+y-1}{\sqrt{2}}$$
이다. 이제 영역 $D_2$에서의 이중적분값을 구할 것인데, 변수변환
$$\begin{cases}
x+y=u \\
x-y=v
\end{cases}$$
를 이용하면
$$u\geq 1,\quad 0\leq v\leq 1$$
이므로
$$\begin{align}
\iint_{D_2} e^{-f(x,y)} dA &= \frac{1}{2}\int_1^{\infty} \int_0^1 e^{-\frac{u-1}{\sqrt{2}}}dvdu \\
&= \frac{\sqrt{2}}{2}
\end{align}$$
이다.
iii) 초록색 영역 $D_3$의 경우, $D_2$에서 했던 것처럼 점을 고른 뒤 원을 그리면 점 $(1, 0)$에 가장 먼저 닿게 된다.
따라서 영역 $D_3$에서 함수 $f(x,y)$는
$$f(x,y)=\sqrt{(x-1)^2 + y^2}$$
이다. 이제 영역 $D_3$에서의 이중적분값을 구할 것인데, 변수변환
$$\begin{cases}
x-1=u \\
y=v
\end{cases}$$
를 이용하면
$$u\geq 0, \quad 0\leq v\leq u$$
이므로
$$\begin{align}
\iint_{D_3} e^{-f(x,y)} dA &=\int_0^{\infty} \int_0^{u} e^{-\sqrt{u^2 + v^2}}dvdu \\
&= \int_0^{\frac{\pi}{4}}\int_0^{\infty} re^{-r}drd\theta \\
&= \frac{\pi}{4}
\end{align}$$
이다.
이상의 결과와 대칭성을 이용하면 주어진 이중적분은
$$\begin{align}
\text{(Integral)} &= 8\left(\frac{1}{4} + \frac{\sqrt{2}}{2} + \frac{\pi}{4}\right) \\
&= 2 + 4\sqrt{2} + 2\pi
\end{align}$$
이다.
2024 가천대학교 편입수학 기출문제 25번 풀이
가속도 벡터 $a$와 단위접선벡터 $T$, 단위법선벡터 $N$에 대하여
$$a = \alpha T + \beta N$$
을 만족시키는 $\alpha, \beta$가 있을 때 $\alpha$를 접선 성분, $\beta$를 법선 성분이라 한다.
또,
$$\begin{cases}
\alpha = \frac{r' \circ r''}{|r'|} \\
\beta = \frac{|r' \times r''|}{|r'|}
\end{cases}$$
이 성립한다.
이제 주어진 점은 $t=1$일 때이고
$$\begin{align}
r'(1) &= (1, 5, 2) \\
r''(1) &= (-1,2,-1)
\end{align}$$
이므로
$$\alpha=\frac{7}{\sqrt{30}}, \beta =\frac{\sqrt{131}}{\sqrt{30}}$$
이다. 따라서
$$\alpha+\beta = \frac{7+\sqrt{131}}{\sqrt{30}}$$
이다.
마치며
이상으로 2024 가천대학교 편입수학 기출문제 정답 및 해설을 마치겠습니다.
오류, 오타 또는 궁금하신 점이 있으시면 댓글로 남겨주세요~
년도별 가천대학교 편입수학 정답 및 해설 (클릭시 이동)
- 2014 가천대학교 편입수학 기출문제 정답 및 해설
- 2015 가천대학교 편입수학 기출문제 정답 및 해설
- 2016 가천대학교 편입수학 기출문제 정답 및 해설
- 2017 가천대학교 편입수학 기출문제 정답 및 해설
- 2018 가천대학교 편입수학 기출문제 정답 및 해설
- 2019 가천대학교 편입수학 기출문제 정답 및 해설
- 2020 가천대학교 편입수학 기출문제 정답 및 해설
- 2021 가천대학교 편입수학 기출문제 정답 및 해설
- 2022 가천대학교 편입수학 기출문제 정답 및 해설
- 2023 가천대학교 편입수학 기출문제 정답 및 해설
- 2024 가천대학교 편입수학 기출문제 정답 및 해설 (현재)
'편입수학 기출문제 풀이 > 가천대' 카테고리의 다른 글
| [편입] 2023 가천대학교 편입수학 기출문제 정답 및 해설 (풀이) (2) | 2023.11.13 |
|---|---|
| [편입] 2022 가천대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2023.10.08 |
| [편입] 2021 가천대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2023.09.26 |
| [편입] 2020 가천대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2023.09.25 |
| [편입] 2019 가천대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2023.09.23 |